dynamical_matrix.cpp File Reference

Definitions corresponding to dynamical_matrix.hpp. More...

#include <iostream>
#include <complex>
#include <cmath>
#include <constants.hpp>
#include <utilities.hpp>
#include <periodic_table.hpp>
#include <dynamical_matrix.hpp>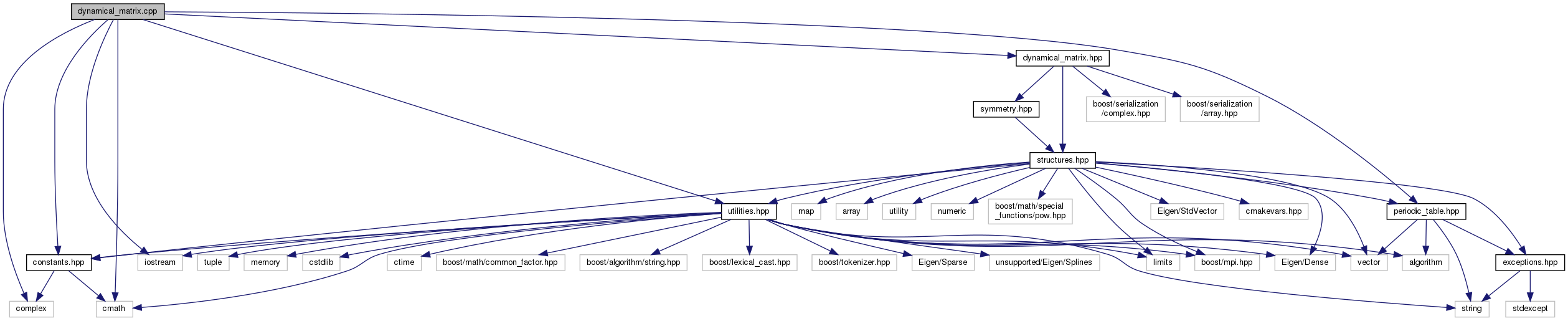

Include dependency graph for dynamical_matrix.cpp:

Classes
class	alma::Atom_pair
	POD class representing a pair of atoms - one in unit cell (0, 0, 0) the other in an arbitrary unit cell cj, and the image of the latter in a number of unit cells cjp. More...

Functions
Eigen::ArrayXXd	alma::build_mass_matrix (const Crystal_structure &structure)
	Return a square matrix with 3 * natoms rows where element ij is equal to the square root of the products of the masses of atom i/3 and atom j/3. More...
std::vector< Atom_pair >	alma::get_normal_pairs (const Crystal_structure &structure, const Harmonic_ifcs &fcs, int na, int nb, int nc)
	Find all atom pairs in a Wigner-Seitz representation of an na x nb x nc supercell. More...
template<typename T >
T	alma::eigen_pairwise_sum (std::vector< T > &v)
	Pairwise summation of a vector of matrices or arrays. More...
Eigen::MatrixXcd	alma::solve_degeneracy (const Eigen::Ref< const Eigen::MatrixXcd > &pert, const Eigen::Ref< const Eigen::MatrixXcd > &eigvecs)
	Choose a unique base of eigenvectors in a degenerate subspace using perturbation theory. More...

Detailed Description

Definitions corresponding to dynamical_matrix.hpp.

Function Documentation

build_mass_matrix()

Eigen::ArrayXXd alma::build_mass_matrix

(

const Crystal_structure &

structure

)

Return a square matrix with 3 * natoms rows where element ij is equal to the square root of the products of the masses of atom i/3 and atom j/3.

Parameters

[in]

structure

- structure of the unit cell

Returns

- the aforementioned square matrix

eigen_pairwise_sum()

template<typename T >

T alma::eigen_pairwise_sum

(

std::vector< T > &

v

)

Pairwise summation of a vector of matrices or arrays.

This reduces the expected error versus a standard summation.

Parameters

[in,out]

v

- vector of operands. All of them must have the same size. The vector will be overwritten.

Returns

the result of the sum

get_normal_pairs()

std::vector<Atom_pair> alma::get_normal_pairs	(	const Crystal_structure &	structure,
		const Harmonic_ifcs &	fcs,
		int	na,
		int	nb,
		int	nc
	)

Find all atom pairs in a Wigner-Seitz representation of an na x nb x nc supercell.

Parameters

[in]	structure	- description of the unit cell
[in]	fcs	- Harmomic_ifcs object adapted to the supercell

Returns

- a vector of Atom_pair

solve_degeneracy()

Eigen::MatrixXcd alma::solve_degeneracy	(	const Eigen::Ref< const Eigen::MatrixXcd > &	pert,
		const Eigen::Ref< const Eigen::MatrixXcd > &	eigvecs
	)

Choose a unique base of eigenvectors in a degenerate subspace using perturbation theory.

Given an arbitrary basis of a degenerate eigenvector space and a suitable perturbation matrix, this function applies an orthogonal transformation to the basis so that the perturbation does not mix the states of the final basis.

Parameters

[in]	dDdq	- perturbation matrix (normally related to a group velocity operator)
[in,out]	eigvecs	- original basis

Returns

the new basis